03 cirkels

Leerdoelen
  1. De leerling is in staat om een ingeschreven en omgeschreven cirkel in Geogebra te construeren.
  2. De leerling is in staat om het middelpunt van een gegeven cirkel bepalen.
  3. De leerling is in staat om de afstanden tussen lijnen/punten en cirkels te laten berekenen door geogebra.
  4. De leerling is in staat om de raaklijn aan cirkels door Geogebra algebraïsch te laten berekenen.
AFSPRAAK OVER NAAMGEVING BESTANDEN
Aan het eind van deze pagina kun je je antwoorden uploaden. Je zult altijd één, of meer GeoGebra bestanden en één Word, of PDf bestand met antwoorden op vragen hebben. Alle vragen/acties gemarkeerd met een ► dienen uitgevoerd te worden en vastgelegd in een WORD of PDF bestand

  • Bewaar je GeoGebra bestanden als 03-cirkels–1.ggb en 03-cirkels–2.ggb etc.
  • Bewaar je Word/Pdf bestand met antwoorden als 03-cirkels.doc(x) en/of 03-cirkels.pdf .

Veel succes!

De opdracht begint hier:

Stelling van Thales

We gaan de stelling van Thales nabouwen.

Daar hebben we eerst de diameter voor nodig.
►Teken een cirkel, deze mag willekeurig getekend worden, maar het makkelijkst is één van de opties waarbij je al een middelpunt hebt (de diameter gaat immers door het middelpunt.).
►Als je cirkel c hebt, met middelpunt M, teken dan (als je dit nog niet hebt) een punt A op de cirkel.
►Teken door A en M een lijn f (of halve rechte). Zet nu in het tweede snijpunt van lijn f met de cirkel een B. AB is nu de diameter.
►Bedenk zelf hoe je dit met puntsymmetrie had kunnen doen.
►Teken nu een willekeurig punt C op de cirkel en teken driehoek ABC. Laat Geogebra hoek C berekenen. Zie je de stelling van Thales? Beweeg punt C ook rond op de cirkel.

Omgekeerde stelling van Thales

►Teken een rechthoekige driehoek ABC, waarbij hoek B de rechte hoek is (dit kan met drie lijnstukken, of met de veelhoek functie).
►Probeer nu met de optie “Cirkel door drie punten” een cirkel c door de drie hoekpunten van ABC te tekenen.
►Lukt dit? Zie je Thales?
►Bepaal het midden van AC. Dit moet nu ook het middelpunt van de cirkel zijn.
►Herken je het middelpunt in de formule van cirkel c?
►Kun je het middelpunt van de cirkel construeren met behulp van koordes? (Zie les over CIRKELS IN MEETKUNDE)
►Probeer ABC te “veranderen”. Blijft de cirkel door de drie hoekpunten gaan? Heb je nu de stelling.

Raaklijnen aan cirkels

►Teken een cirkel c1 met een willekeurig middelpunt M1 en een straal van 3.
►Kies een punt A op de cirkel en teken de halfrechte M1A.
►We willen een cirkel c2 tekenen met middelpunt M2 en straal 5 die cirkel c1 raakt in punt A.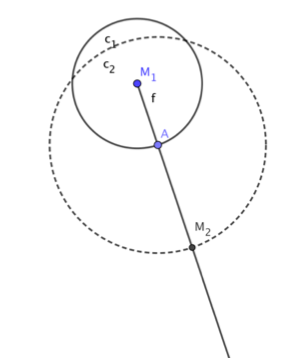
►Construeer de plaats van M2 met een hulpcirkel met als middelpunt A

 

en straal 5. (Zie afbeelding)

 

 

 

 

 

 

 

 

 

►Je kunt nu cirkel c2 tekenen die c1 raakt in punt A.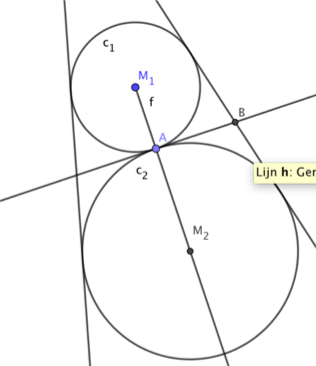
►Teken nu de raaklijnen van cirkels c1 en c2, je ziet er drie als het goed is!
►Noem het snijpunt van de raaklijn door punt A en één van de raaklijnen aan beide cirkels punt B. Je krijgt afbeelding 2.
►Bereken de afstand AB en vergelijk deze met de afstand die je meet in geoGebra.

 

 

 

 

Oppervlaktes binnen een cirkel

►Construeer een cirkel met middelpunt M en straal 5.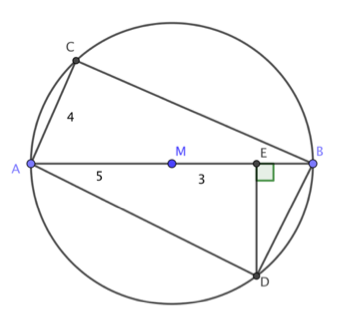 ►Teken in de cirkel de vierhoek ABCD als hiernaast.

  • MA=5
  • ME=3
  • AC=4
  • ED⊥AB

Voor het vinden van Punt C en E is een hulpcirkel gebruikt.

 

 

 

 

 

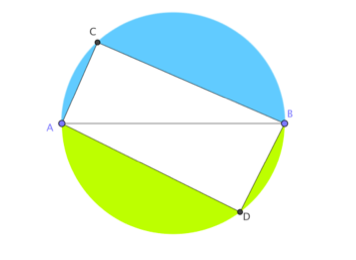
►Bereken het verschil tussen het groene en blauwe deel.

(Tip 1: Als je dit met GeoGebra wilt doen kan de “Cirkelsector door drie punten” van pas komen!)
(Tip 2: trek ABCD over met een “Veelhoek”.)

 

 

 

 

 

 

Upload je bestanden hier
[wordpress_file_upload singlebutton=”true” dragdrop=”false” uploadrole=”all” uploaduser=”all” uploadpatterns=”*.pdf, *.doc, *.docx, *.ggb” forcefilename=”true” duplicatespolicy=”maintain both” placements=”filename+selectbutton/progressbar/subfolders/filelist” uploadtitle=”Upload bestanden” selectbutton=”Selecteer bestanden/Selecteer bestanden” uploadbutton=”Selecteer bestanden/Selecteer bestanden”] [wordpress_file_upload_browser pagination=”false” bulkactions=”false” candownload=”true” candelete=”true” deletestrictmode=”true” columns=”file:s/File,date:n/Upload Date,user:s/User,link:/Link” postfilter=”current”]