- De leerling is in staat om een middenparallel, hoogtelijnen en zwaartelijnen in Geogebra te visualiseren.
- De leerling is in staat om stellingen over middenparallel, hoogtelijnen en zwaartelijn te visualiseren.
- Bewaar je GeoGebra bestanden als 04-bewijzen-in-driehoeken–1.ggb en 04-bewijzen-in-driehoeken–2.ggb etc.
- Bewaar je Word/Pdf bestand met antwoorden als 04-bewijzen-in-driehoeken.doc(x) en/of 04-bewijzen-in-driehoeken.pdf .
Veel succes!
De opdracht begint hier:
► Teken in geogebra een willekeurige driehoek ABC en teken de middenparallellen PQ, QR en PR.
► Welke eigenschappen heeft een middenparallel? Leg uit hoe je in geogebra een midden van een zijde kan laten bepalen.
► Bewijs dat een middenparallel gelijk is aan de helft van de zijde waaraan die evenwijdig is (Hint: Gebruik gelijkvormigheid van driehoeken).
Bekijk de film voor hints:
► Teken in geogebra een willekeurige driehoek ABC en teken de zwaartelijnen AD, BE en CF.
► De drie zwaartelijnen lijken door één punt te gaan. Is dit bij elke driehoek zo?
► De zwaartelijnen snijden elkaar in stukken. Bestaat er een specifieke verhouding tussen de stukken? Met andere woorden: Als je het snijpunt van de zwaartelijnen S noemt, kun je dan wat vertellen over AS:AD?
► Bewijs dat de verhouding waarin de zwaartelijnen elkaar snijden altijd 2:1 is.
Gebruik gelijkvormigheid van driehoeken en verhoudingen (Hint: Teken eerst een middenparallel om gelijkvormige driehoeken te kunnen vinden).
► Gebruik het vorige bewijs om te bewijzen dat de zwaartelijnen door één punt gaan.
Bekijk de film voor hints:
►Teken in geogebra een willekeurige scherphoekige driehoek ABC en teken de hoogtelijnen CD, AF en BE.
►Sleep één van de hoekpunten van driehoek ABC zodanig, dat je een stomphoekige driehoek krijgt.
►Waarom verdwijnen er hoogtelijnen? Hoe volgt dat uit de definitie van een hoogtelijn? En welke beperking van geogebra moet je dus oplossen?
►Construeer de driehoek in geogebra zodanig, dat je de hoekpunten kunt blijven verslepen en de hoogtelijnen altijd zichtbaar blijven. AB, BC en AC zijn de middenparallellen van een grotere driehoek PQR. (Gebruik in geogebra de functie ‘evenwijdige rechte’ om dit voor elkaar te krijgen.)
Je eindigt met de afbeelding hiernaast: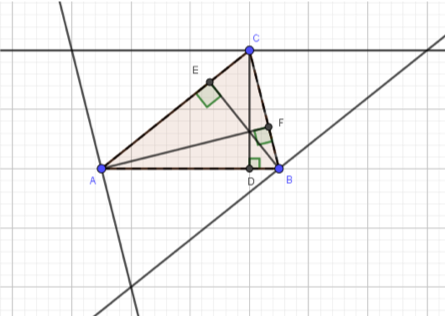
►Noem de grote driehoek PQR en leg uit dat de getekende hoogtelijnen van driehoek ABC de middelloodlijnen zijn van driehoek PQR.
►Teken met behulp van het snijpunt van de middelloodlijnen de omgeschreven cirkel van driehoek PQR.
►Hoe zou het voorgaande je kunnen helpen te bewijzen dat de drie hoogtelijnen van een driehoek altijd door één punt gaan?
Bekijk de film voor hints:
Eindopdracht:
Bekijk eerst de film:
►Gegeven: ∆ABC met hoogtepunt H en middelpunt van de omgeschreven cirkel O, met O binnen ∆ABC.
►Te bewijzen: ∠BAH=∠CAO.
►Gebruik geogebra om driehoeken te maken en vermoedens te checken!
►Wanneer je punt O buiten de driehoek kiest, kun je dan op dezelfde manier bewijzen dat ∠BAH=∠CAO? Of zul je een andere aanpak moeten kiezen?