[su_box title=”Leerdoelen” box_color=”#39b632″]
- De leerling is in staat om isometrieën in Geogebra te construeren.
- De leerling is in staat om samenstellingen van isometrieën in Geogebra te verklaren.
[/su_box]
[su_box title=”AFSPRAAK OVER NAAMGEVING BESTANDEN” box_color=”#b2231c”]
Aan het eind van deze pagina kun je je antwoorden uploaden. Je zult altijd één, of meer GeoGebra bestanden en één Word, of PDf bestand met antwoorden op vragen hebben. Alle vragen/acties gemarkeerd met een ► dienen uitgevoerd te worden en vastgelegd in een WORD of PDF bestand
- Bewaar je GeoGebra bestanden als [su_post field=”post_name”]-1.ggb en [su_post field=”post_name”]-2.ggb etc.
- Bewaar je Word/Pdf bestand met antwoorden als [su_post field=”post_name”].doc(x) en/of [su_post field=”post_name”].pdf .
Veel succes![/su_box]
De opdracht begint hier:
Bekijk de film:
Symmetrie
De volgende logo’s of symbolen hebben een symmetrie in zich.
► Kan jij bepalen welke verschillende symmetrieën de logo’s/symbolen in zich hebben?
Vlakvullingen
Een vlakvulling is opgebouwd aan de hand van een aantal basisfiguren. Door het toepassen van verschillende symmetrieën ontstaat er een vlakvulling.
► Open het GeoGebra-bestand vlakvullingen.ggb en maak van de verschillende basisfiguren een vlakvulling doormiddel van het toepassen van verschillende symmetrieën.
► Bij welke figuren lukt dit wel en met welke symmetrieën?
► Kan je ook bedenken waarom?
Isometrie
Bekijk het filmpje over isometrie.
► Wat is een isometrie?
Samenstellingen van isometrieën
Symmetrieën werken op meetkundige figuren via transformaties, die je kunt samenstellen. In onderstaande tabel staan de symmetrieën van de zespuntige werpster (Geogebra-bestand samengestelede isometrieën 1.ggb).
A: Rotatie met de klok mee over 0◦
B: Rotatie met de klok mee over 60◦
C: Rotatie met de klok mee over 120◦
D: Rotatie met de klok mee over 180◦
E: Rotatie met de klok mee over 240◦
F: Rotatie met de klok mee over 300◦
In de vermenigvuldigingstabel wordt een verticale symmertie eerst uitgevoerd, daarna een horizontale.
► Vul de tabel verder in gebruik GeoGebra ter controle.
| * | A | B | C | D | E | F |
| A | ||||||
| B | ||||||
| C | ||||||
| D | ||||||
| E | ||||||
| F |
► Doe hetzelfde voor een gelijkzijdige driehoek, waarbij:
I: Rotatie met de klok mee over 0◦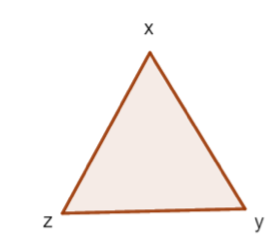
II: Rotatie met de klok mee over 60◦
III: Rotatie met de klok mee over 120◦
A: Spiegeling in lijn door x.
B: Spiegeling in lijn door y.
C: Spiegeling in lijn door z.
| * | I | II | III | A | B | C |
| I | ||||||
| II | ||||||
| III | ||||||
| A | ||||||
| B | ||||||
| C |
Eindopdracht
► Vul het overzicht van samengestelde isometrieën in.
| * | Identiteit | Translatie | Lijnspiegeling | Rotatie | Glijspiegeling |
| Identiteit | |||||
| Translatie | |||||
| Lijnspiegeling | |||||
| Rotatie | |||||
| Glijspiegeling |
[su_box title=”Upload je bestanden hier” box_color=”#9db5e4″]
[wordpress_file_upload singlebutton=”true” dragdrop=”false” uploadrole=”all” uploaduser=”all” uploadpatterns=”*.pdf, *.doc, *.docx, *.ggb” forcefilename=”true” duplicatespolicy=”maintain both” placements=”filename+selectbutton/progressbar/subfolders/filelist” uploadtitle=”Upload bestanden” selectbutton=”Selecteer bestanden/Selecteer bestanden” uploadbutton=”Selecteer bestanden/Selecteer bestanden”]
[wordpress_file_upload_browser pagination=”false” bulkactions=”false” candownload=”true” candelete=”true” deletestrictmode=”true” columns=”file:s/File,date:n/Upload Date,user:s/User,link:/Link” postfilter=”current”]
[/su_box]