- De leerling is in staat om grafieken van verschillende functies in Geogebra te plotten en te analyseren door gebruik van opties als snijpunt bepalen.
- De leerling is in staat om families van functies in Geogebra te plotten door gebruik van extra parameter(s) en schuifknop(pen).
- De leerling is in staat een tekstvak te genereren dat een dynamisch functievoorschrift bevat.
- De leerling is in staat om Geogebra de inverse van een getekende functie te laten plotten.
- De leerling kan Geogebra gericht inzetten ter ondersteuning en visualisering van wiskundige probleemstellingen.
- Bewaar je GeoGebra bestanden als 10-functies-en-grafieken–1.ggb en 10-functies-en-grafieken–2.ggb etc.
- Bewaar je Word/Pdf bestand met antwoorden als 10-functies-en-grafieken.doc(x) en/of 10-functies-en-grafieken.pdf .
Veel succes!
De opdracht begint hier:
In geogebra kunnen we ook grafieken laten tekenen en daarbij berekeningen laten uitvoeren.
► Voer in de invoerbalk in: y=x²+5x-3.
Let op: x² voer je in als x^2
Je ziet de functie nu aan de linkerkant in je algebravenster verschijnen als een kegelsnede. Je kunt de vorm van de formule van de kegelsnede aanpassen door met je rechtermuisknop te klikken op de functie en een andere vorm te selecteren:
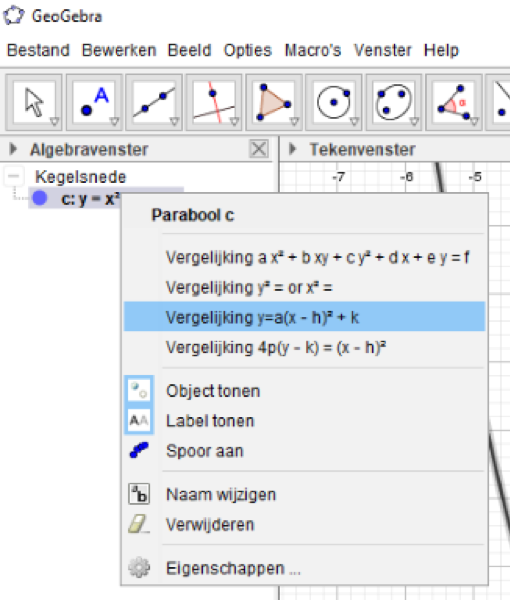
► Laat met behulp van kwadraatafsplitsen zien dat de formule, die geogebra geeft, de juiste is.
Geogebra kan allerlei functies plotten, maar daar zijn soms commando’s voor nodig. Gelukkig zijn de meesten voor de hand liggend:
► Plot de grafiek van y=||x-2|-2| door de volgende invoer: y=abs(abs(x-2)-2)
(Zorg ervoor dat de grafiek van y=x²+5x-3 ook nog steeds geplot is.)
► Bereken de snijpunten van beide grafieken door een vergelijking op te lossen. (Controleer je antwoord door het commando ‘snijpunten’ in geogebra te gebruiken.)
Een dynamisch punt tekenen en de grafiek laten schetsen.
► Plot de grafiek van y=x²-2 en:
► Gebruik het commando ‘punt’ en voer in P=punt((x-4)²-2). Geogebra tekent nu een punt op de parabool y=(x-4)²-2.
► Rechtsklik op het punt en selecteer ‘spoor aan’.
► Beweeg nu het punt heen en weer of rechtsklik op het punt en klik op ‘animatie aan’. De animatie kun je stopzetten door in je scherm linksonder op pauze te klikken.
Het valt je misschien op dat de getekende parabool die het punt P maakt, eigenlijk een verschuiving is van de parabool y=x²-2.
► Om geogebra ons de familie van parabolen y=(x-a)²-2 te laten tekenen, voeren we in y=(x-a)²-2 in. Geogebra vraagt je nu om een schuifknop te maken van de variabele a.
We kunnen de formule van de parabool y=(x-a)²-2 ook weergeven als dynamische tekst. Dit doen we als volgt:
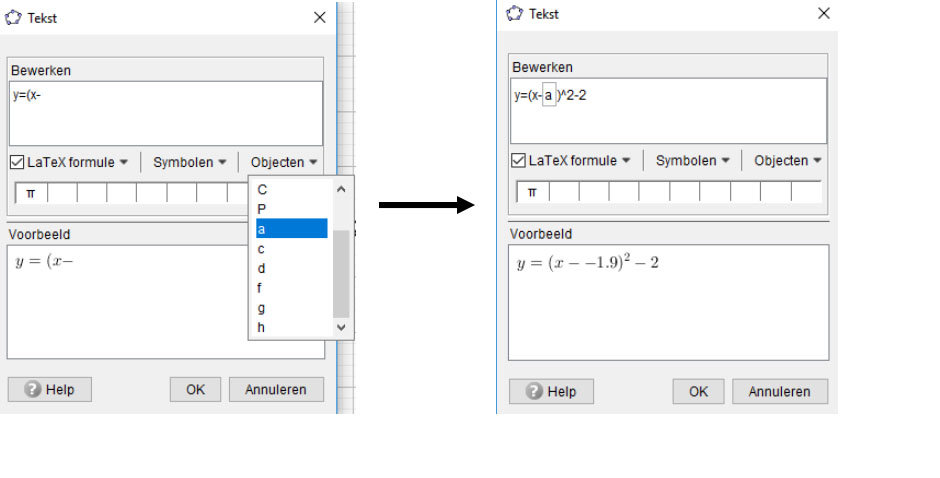
► Selecteer een tekstvak, selecteer de optie LaTeX-formule en type de formule in.
Let op: omdat we werken met een afhankelijke variabele a, moeten we die selecteren bij de opties (zie screenshot hieronder).
Je kunt dit tekstvak verder opmaken door in het menu van de rechtermuisknop eigenschappen te kiezen.
► Open het bestand machtsfuncties.ggb.
► Bekijk hoe het bestand werkt.
► Maak een zelfde bestand waarmee je de familie van exponentiële functies
y=a+b∙g^(t-c) door middel van parameters (schuifknoppen) goed in beeld kan brengen.
► Waarom geeft g<0 je geen grafiek?
► Wat gebeurt er als 0<g<1, g>1 of g=1? Verklaar aan de hand van de formule.
Inversen in geogebra
Om een inverse van een gegeven functie te bepalen maak je gebruik van de symmetrie in de lijn y=x. Vervolgens maak je de variabele y weer vrij en heb je het voorschrift van de inverse functie bepaald.
Dit kun je in geogebra ook meetkundig laten doen.
► Hiervoor voer je de functie y=x² in en laat de parabool tekenen.
► Teken ook de lijn y=x.
► Gebruik nu de knop lijnspiegeling en spiegel de parabool in de lijn y=x.
► Waarom moet je wel rekening houden met het domein van de (inverse) functie?
► Leg dit ook uit door uit de parametervoorstelling t te elimineren.
► Maak een plot van de volgende opdracht in geogebra en ga eerst experimenteren om een gevoel voor de opdracht en het proces te krijgen. Ga dan aan de slag met algebraïsch oplossen.
► Voor elke a en b, met a≠b, is gegeven de functie f(x)=(ax+b)/(x+1).
► Bereken algebraïsch voor welke a en b de grafieken van f en zijn inverse elkaar snijden in de punten A(3,y_1) en B(5,y_2) (de x-coördinaten zijn dus bekend en de y-coördinaten onbekend (of juist niet?)).
Hulpbestand opdracht inverse.ggb (alleen gebruiken als je het niet lukt het bestand zelf te maken).
Afsluitende opdracht
► Voor elke a≠2 2/5 is gegeven de functie f(x)=(ax-4)/(3x-5).
► Bekijk in geogebra en bereken algebraïsch voor welke a
- De lijn y=1 horizontale asymptoot is van de grafiek van f.
- De lijn x=2 verticale asymptoot is van de grafiek van de inverse van f.
- De functie g(x)=(5x-4)/(3x-7) de inverse is van f.
- De grafieken van f en zijn inverse geen gemeenschappelijke punten hebben.