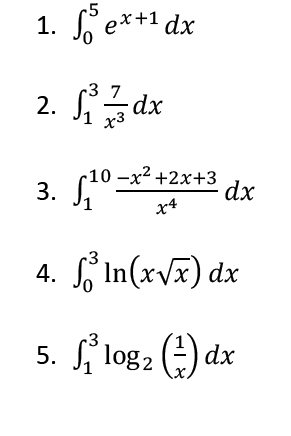- De leerling kan met behulp van de Riemann som de oppervlakte onder gegeven functies bepalen.
- De leerling kan een gegeven Geogebra bestand analyseren en de werking ervan uitleggen aan anderen.
- Bewaar je GeoGebra bestanden als 12-integraal–1.ggb en 12-integraal–2.ggb etc.
- Bewaar je Word/Pdf bestand met antwoorden als 12-integraal.doc(x) en/of 12-integraal.pdf .
Veel succes!
De opdracht begint hier:
Riemann som
bekijk de film over de Riemann Som:
► Download het bestand Riemann.ggb
► Experimenteer met het bestand. Kijk of je iets kunt leren van de opbouw in het Algebra venster
► Bereken zelf de oppervlakte onder de volgende functies en controleer dit met de Riemann Som.
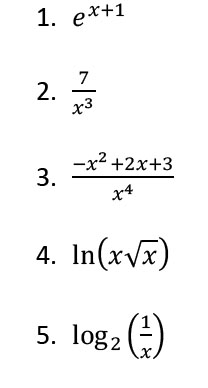
Oppervlakte onder
► bereken de volgende integralen (controleer met Riemann.ggb)
Integralen tussen
►Bereken de rode oppervlakte (controleer met GeoGebra’s integraaltussen commando) (kun je het ook met Riemann.ggb controleren?)
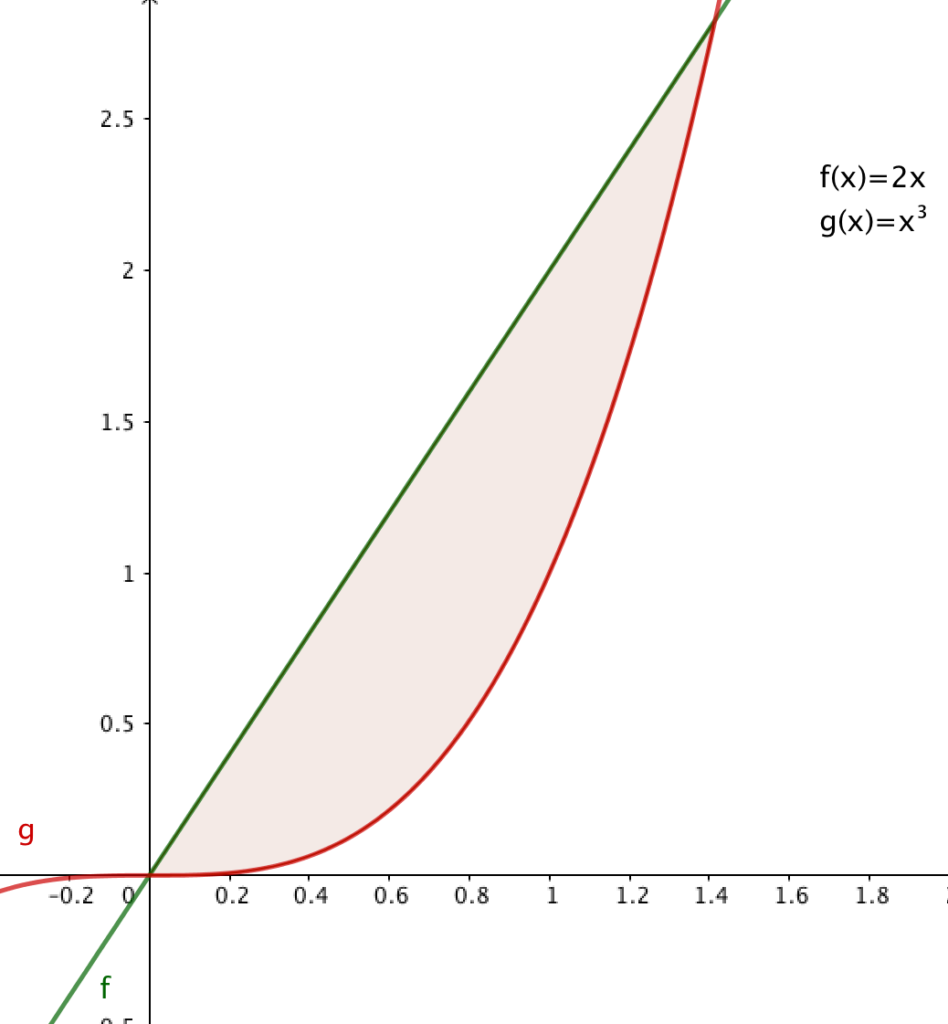
►Bereken de rode oppervlakte (controleer met GeoGebra’s integraaltussen commando) (kun je het ook met Riemann.ggb controleren?)
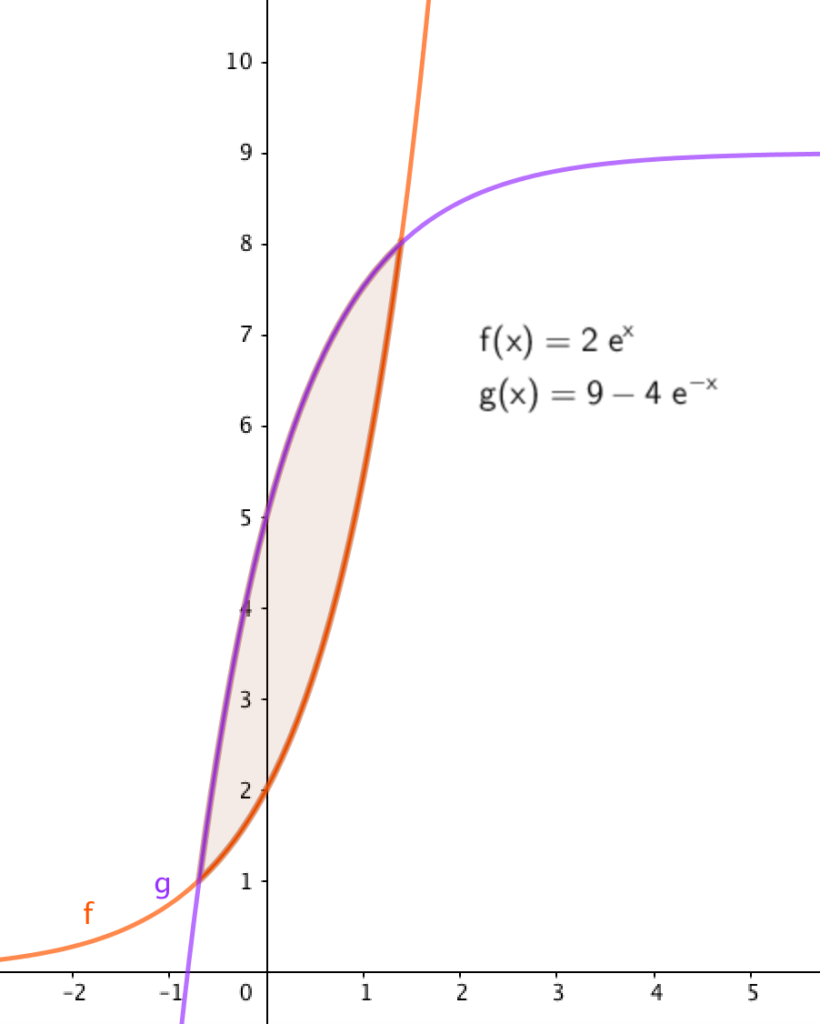
► De formule van de eenheidscirkel (x²+y²=1)is een formule met twee variabelen en niet geschikt voor de integraal, maar je kunt wel een formule opstellen in de vorm van y=… doet dat eens!
► Plot die formule eens met GeoGebra en bedenk wat de oppervlakte van deze figuur zou moeten zijn.
► Controleer dat met GeoGebra.