- De leerling is in staat om een ingeschreven en omgeschreven cirkel in Geogebra te construeren.
- De leerling is in staat om het middelpunt van een gegeven cirkel bepalen.
- De leerling is in staat om de afstanden tussen lijnen/punten en cirkels te laten berekenen door geogebra.
- De leerling is in staat om de raaklijn aan cirkels door Geogebra algebraïsch te laten berekenen.
- Bewaar je GeoGebra bestanden als 16-cirkels–1.ggb en 16-cirkels–2.ggb etc.
- Bewaar je Word/Pdf bestand met antwoorden als 16-cirkels.doc(x) en/of 16-cirkels.pdf .
Veel succes!
De opdracht begint hier:
Invoeren vergelijking voor cirkel
► Voer de volgende functie in bij GeoGebra en kijk of de cirkel wordt getekend die je verwacht.
(x-3)²+(y+4)²=16
Middelpunt cirkel vinden
Hoe vind je een middelpunt van een cirkel?
► Teken op de cirkel van vraag drie willekeurige punten A, B en C.
► Teken de koordes AB en BC en de middelloodlijn van die koordes.
► In welk punt snijden ze elkaar?
► Had je dat verwacht? Leg uit!
Straal cirkel bepalen en vergelijking omschrijven
Hoe vind je de straal van een cirkel als deze niet mooi door roosterpunten gaat?
► Zoek eerst het middelpunt, noem deze M.
► Meet nu de afstand MA, of MB, of MC (een van de drie punten die je hebt gebruikt bij het bepalen van het midden) met de afstand functie bovenin, of tik bij de invoer: Afstand (A, B).
► Probeer het eens bij:
x²+y²+6x+8y+9=0
► Was het was je verwachtte?
► Kijk in het algebra venster en schrijf de kegelsnede (rechtermuis) om naar de functie (x-m)²+(y-n)²=r². Je herkent als het goed is de straal en het middelpunt.
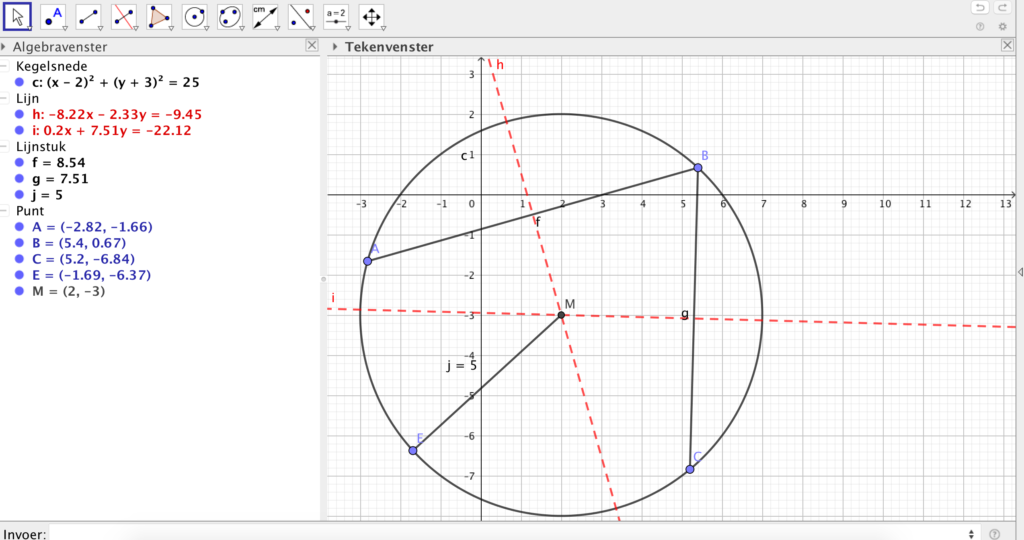
Vergelijkingen cirkels
► Schrijf de volgende functie met behulp van kwadraat afsplitsen om naar de vorm (x-a)²+(y-b)²=r²
x²+y²+8x-14y+49=0
► Voer de functie in en kijk of je de cirkel krijgt die je verwacht.
► Verander de ook in het algebravenster (rechtermuisknop) de kegelsnede formule naar een vergelijking. Klopt deze?
Afstand tussen lijnen/punten en cirkels zijn makkelijk te meten in Geogebra.
► Teken een cirkel met middelpunt M (2,1) en straal 3 in GeoGebra (kies hiervoor de “Cirkel met middelpunt en straal” functie.
► Teken ook punt A (5,5). Bereken eerst algebraïsch de afstand d (M,A).
► Bereken de afstand in GeoGebra door een halfrechte van M naar A te tekenen en zoek het snijpunt met de cirkel. Noem dit punt B. Meet, of bereken nu d (A,B).
► Klopt het?
Geogebra kan je helpen bij het berekenen van de functies van raaklijnen aan cirkels.
► Bepaal algebraïsch de vergelijking van de raaklijn van lijn l die cirkel c:(x-3)²+(y-1)²=5 raakt in punt A(2,-1).
► Voer nu de vergelijking c in bij GeoGebra en teken punt A op de cirkel.
► Bepaal met de functie raaklijnen van Geogebra de raaklijn aan cirkel c in punt B. (je krijgt een lijn f, schrijf die om naar y=ax+b door in het Algebra venster met de rechtermuisknop op f te klikken)
► Klopt het met wat jij had?
Snijpunten van lijnen met cirkels schatten met behulp van parameters
► Teken een cirkel c: (x-5)² + (y-1)²=17 en een lijn f: y=4x+q en laat GeoGebra schuifknoppen voor q tekenen.
► Laat het interval van de schuifknop q (rechtermuis) van -40 tot 0 lopen.
► Probeer met de schuifknop te bepalen voor welke twee waarden van q de lijn f aan de cirkel c raakt.
► Bepaal hierna algebraïsch de oplossingen (dit is een hele klus)