- De leerling kan het 3D venster gebruiken om kegelsneden in drie dimensies te tekenen.
- De leerling kan in Geogebra verschillende ruimtelijke figuren tekenen.
- De leerling kan in Geogebra doorsneden van een ruimtelijk figuur laten tekenen.
- De leerling kan in Geogebra de doorsnede van een variabel vlak met een kegel laten tekenen.
- Bewaar je GeoGebra bestanden als 18-kegelsnedes–1.ggb en 18-kegelsnedes–2.ggb etc.
- Bewaar je Word/Pdf bestand met antwoorden als 18-kegelsnedes.doc(x) en/of 18-kegelsnedes.pdf .
Veel succes!
De opdracht begint hier:
Kegelsnedes in 3D
 Voor een prachtige presentatie over kegelsnedes verwijzen we jullie naar deze GeoGebra applet.
Voor een prachtige presentatie over kegelsnedes verwijzen we jullie naar deze GeoGebra applet.
► Download hem ook hier: Kegelsnedes 3D.ggb
► “Speel” met de applet en zorg ervoor dat de weer precies begrijpt wanneer bepaalde kegelsnedes ontstaan en welke het zijn. (Het zijn er 4)
GeoGebra heeft inderdaad een 3D venster. Deze werkt echter nog wat gemankeerd en lastig naar onze smaak, dus we beperken ons tot de functies van de 4 kegelsnedes. In de les van CONFLICTLIJNEN heb je al het een en ander geleerd over conflictlijnen, maar we gaan er nog even mee door.
Ellips als meetkundige plaats
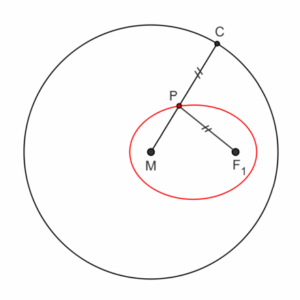
- Een ellips is de meetkundige plaats van alle punten waarvan de som van de afstanden tot twee vaste punten (de brandpunten) constant is.
- Een ellips is de verzameling van alle punten met gelijke afstanden tot een cirkel en een punt BINNEN de cirkel (zie tekening)
Bekijk de film over de Ellips als meetkundige plaats
► Bouw het bestand om de ellips als meetkundige plaats te vinden na.
► Oefen met de functie Ellips[] in Geogebra.
Hyperbool als meetkundige plaats
- Een hyperbool is de meetkundige plaats van alle punten waarvan het verschil van de afstanden tot twee vaste punten (de brandpunten) constant is.
- Een ellips is de verzameling van alle punten met gelijke afstanden tot een cirkel en een punt BUITEN de cirkel.
► Leg uit waarom en hoe je met hetzelfde bestande de hyperbool als meetkundige plaats kunt laten zien.
► Oefen met de functie Hyperbool[] in Geogebra. Kun je met Hyperbool[] ook een ellips maken? En omgekeerd? Waar ligt het “omslagpunt?
► Hyperbool[] heeft als invoer twee brandpunten en een getal. Wat is de betekenis van dat getal?
► Teken een hyperbool met als brandpunten A(0,0) en B(8,0), hoe groot moet het getal in Hyperbool(A,B,getal) zijn om ook een hyperbool (en geen ellips) te krijgen?
► Wat weet je van de straal van de richtcirkel?
► Teken die richtcirkel en de raaklijnen aan die cirkel vanuit B.
► Teken de raakpunten aan de richtcirkel, noem ze P en Q.
► Teken de middelloodlijnen op BQ en BP.
► Wat stellen die middelloodlijnen voor? (Wat zijn ze van de hyperbool?)
Parabool als meetkundige plaats
- Een parabool is de meetkundige plaats van alle punten waarvoor de afstand tot een vast punt (het brandpunt) en een lijn (de richtlijn) constant is.
Bekijk eerst de film
► Bouw het bestand om de parabool als meetkundige plaats te vinden na.
► Experimenteer met Parabool[F,l] en noteer de formules voor de kegelsnede (parabool)
- Neem F(0,2) en l:y=1
- Neem F(0,1) en l:y=0.5
- Neem F(0,1) en l:y=-1
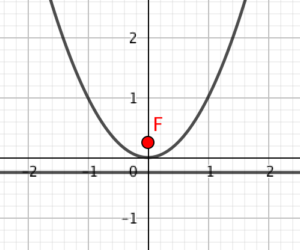 ► Waar moeten F en l liggen om met Parabool[F,l] de kegelsnede c: y=x² te krijgen? (zie afbeelding)
► Waar moeten F en l liggen om met Parabool[F,l] de kegelsnede c: y=x² te krijgen? (zie afbeelding)