- De leerling kan kegelsneden herkennen aan vergelijkingen (binnen Geogebra).
- De leerling kan de functie kegelsneden in Geogebra gebruiken om vergelijkingen van kegelsneden op te stellen.
- De leerling kan de functie kegelsneden in Geogebra gebruiken om de verschillende kegelsneden te tekenen.
- De leerling is in staat om parameters toe te voegen aan de vergelijking voor een kegelsnede om zo een dynamische weergave in beeld te krijgen (die kan worden veranderd met behulp van de schuifknop).
- Bewaar je GeoGebra bestanden als 19-kegelsnedes–1.ggb en 19-kegelsnedes–2.ggb etc.
- Bewaar je Word/Pdf bestand met antwoorden als 19-kegelsnedes.doc(x) en/of 19-kegelsnedes.pdf .
Veel succes!
De opdracht begint hier:
Formule (alle) kegelsnedes
De formule van de kegelsnede is als volgt:
ax² + by² + 2hxy + 2gx + 2fy + c=0
(we hebben a, b, c, f, g en h gekozen zodat we deze parameters hieronder kunnen gebruiken. Pas ze daarom goed toe!)
► Bouw de formule eens na in GeoGebra (inderdaad, je krijgt 5 schuifknoppen!)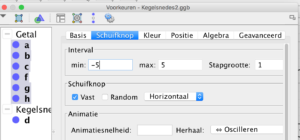
► geef alle schuifknoppen intervallen van -5 tot 5 met stappen van 1.
► Maak er eens een cirkel van.
► Wat moet gelden voor c? Als het goed is zie je dat c een negatief getal moet zijn.
Daarom schrijven we de functie van de kegelsnede maar als volgt
ax² + by² + 2hxy + 2gx + 2fy = c (c mag nu positief zijn)
► Ga één voor één de volgende gevallen eens na in GeoGebra
- h² = ab, is de vergelijking een parabool
- h² < ab, is de vergelijking een ellips,
- h² > ab, is de vergelijking een hyperbool,
- a = b en h = 0, is de vergelijking een cirkel,
- a + b = 0, is het een rechthoekige hyperbool.
► Kloppen ze allemaal?
De Ellips nader beschouwd
► 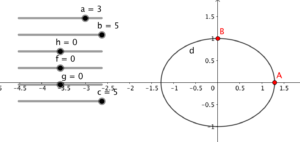 Bouw een ellips door a=3, b=5 en c=5 te kiezen (zie plaatje)
Bouw een ellips door a=3, b=5 en c=5 te kiezen (zie plaatje)
► De formule is 3x² + 5 y² = 5 (oftwel ax² + by² = c)
► Laat zien dat punt A als coordinaten (√(c/a),0) heeft en B (0,√(b/a))
► Laat zien dat de lengteas van de ellips gelijk is aan 2√(c/a).
► 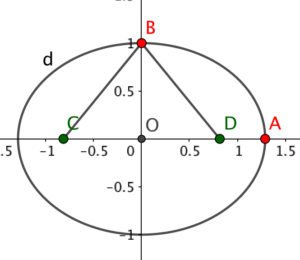 Teken de brandpunten C en D van de ellips met het commando Brandpunten[]
Teken de brandpunten C en D van de ellips met het commando Brandpunten[]
► Beredeneer dat DB+CB=2√(c/a)
► Bereken met behulp van Pythagoras dat OD (en OC) = 2√(c/a-c/b).
► Controleer of de coordinaten van C en D kloppen met wat je in de vorige vraag vond. (Je kunt nu de brandpunten van een ellips dus zelf ook berekenen!)