Leerdoelen

De leerling is in staat het differentiequotiënt binnen Geogebra te benaderen en realiseert zich dat er een limiet wordt toegepast.
De leerling kan Geogebra verschillende afgeleiden laten bepalen en dit simuleren door met behulp van differentiequotiënten afgeleiden te benaderen.
De leerling kan binnen Geogebra de raaklijn aan een gegeven functie in een bepaald punt opstellen.

AFSPRAAK OVER NAAMGEVING BESTANDEN

Aan het eind van deze pagina kun je je antwoorden uploaden. Je zult altijd één, of meer GeoGebra bestanden en één Word, of PDf bestand met antwoorden op vragen hebben. Alle vragen/acties gemarkeerd met een ► dienen uitgevoerd te worden en vastgelegd in een WORD of PDF bestand

Bewaar je GeoGebra bestanden als 11-afgeleide-functie–1.ggb en 11-afgeleide-functie–2.ggb etc.
Bewaar je Word/Pdf bestand met antwoorden als 11-afgeleide-functie.doc(x) en/of 11-afgeleide-functie.pdf .

Veel succes!

De opdracht begint hier:

Differentiequotiënt en de raaklijn aan een functie

►  Teken de grafiek van f(x) = x² – 3x – 4 en punt A(0,-4) en B(4,0).
►  Teken de lijn f door A en B. Waar kun je zien dat de differentiequotiënt gelijk is aan 1?
►  Beweeg nu punt B dichter naar punt A. Wat gebeurt er met de differentiequotiënt?
►  Wat is de richtingscoëfficiënt van de raaklijn aan grafiek f in punt A?
►  Bereken de helling in punt A met behulp van de afgeleide functie. Klopt het met hetgeen je waarnam bij de differentiequotiënt?

De afgeleide functie

De afgeleide functie is gedefinieerd als een differentiequotiënt waarbij de afstand tussen de twee punten naar nul nadert.

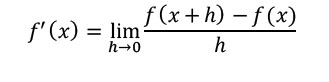
►  We gaan dit proberen voor f(x)=x^3, laat GeoGebra de afgeleide f'(x) tekenen.
►  Voer nu ook de volgende functie in g(x)=(f(x+h)-f(x))/h en maak een schuifknop voor h. Pas de schuifknop aan naar interval 0.00001 tot 10. (Snap je waarom we 0.00001 nemen?)
►  Beweeg de schuifknop naar 0.00001 (er staat waarschijnlijk gewoon 0, maar wees gerust).
►  Zie je dat g(x) de afgeleide functie wordt als h heel klein wordt?

► Verander f(x) nu eens naar:

f(x) = x² – 3x – 4
f(x) = sin⁡(x)
f(x)= 2^x
f(x) = e^x
functies die je zelf wilt bedenken en proberen

Zelf afgeleide functies afleiden

bekijk eerst de video:

► probeer nu zelf met behulp van de differentie quotiënt de afgeleide functies te berekenen van:

3x²+6x-17
cos(x) (hoeksom en hoekverschil) (let op de +/- en de -/+!)
tan(x) (hoeksom en hoekverschil) (let op de +/- en de -/+!)
1/x
e^x (pittig! Bekijk deze pagina en zie of je eruit komt!)

Geogebra kan afgeleides berekenen

► Je weet dat de afgeleide van de ln(x) gelijk is aan 1/x. Voer in geoGebra eens in f(x)=ln(x) en geef een ENTER. Voer nu simpelweg een f’ in als functie. Zie je wat er gebeurt? Handig he?

Upload je bestanden hier

[wordpress_file_upload singlebutton=”true” dragdrop=”false” uploadrole=”all” uploaduser=”all” uploadpatterns=”*.pdf, *.doc, *.docx, *.ggb” forcefilename=”true” duplicatespolicy=”maintain both” placements=”filename+selectbutton/progressbar/subfolders/filelist” uploadtitle=”Upload bestanden” selectbutton=”Selecteer bestanden/Selecteer bestanden” uploadbutton=”Selecteer bestanden/Selecteer bestanden”] [wordpress_file_upload_browser pagination=”false” bulkactions=”false” candownload=”true” candelete=”true” deletestrictmode=”true” columns=”file:s/File,date:n/Upload Date,user:s/User,link:/Link” postfilter=”current”]