- De leerling is in staat om de basisvaardigheden in Geogebra in te zetten ter visualisering van wiskundige problemen.
- De leerling is in staat om de basisvaardigheden in Geogebra in te zetten om wiskundige problemen op te lossen.
- Bewaar je GeoGebra bestanden als 01-meetkunde–1.ggb en 01-meetkunde–2.ggb etc.
- Bewaar je Word/Pdf bestand met antwoorden als 01-meetkunde.doc(x) en/of 01-meetkunde.pdf .
Veel succes!
De opdracht begint hier:
Bekijk de film:
Het standaardtekenvenster van GG is in twee dimensies en dus heel goed geschikt voor vlakke meetkunde.
Punten, lijnen, figuren tekenen
► Teken de punten (2,3) en (5,1).
(Dat kan met de knop [Nieuw punt], maar zet dan eerst het rooster aan.
Het kan ook door achter [Invoer] te typen A=(2,3) en [Enter] en dan B=(5,1) en [Enter]. Probeer beide manieren uit.)
► Teken de lijn door de twee getekende punten.
(Dat kan met de knop [Rechte door 2 punten] of door achter invoer te typen Rechte[A,B]. Je kunt er de knop [Commando] bij gebruiken, nodig is dat niet.)
► Klik met de rechter muisknop op de lijn AB. Kies: Eigenschappen. Kies bij Toon label voor Naam & Waarde. Je krijgt nu de letter die bij de lijn hoort en de vergelijking te zien.
(Je hebt wel gezien dat je door met de rechter muisknop op een object te klikken allerlei zaken kunt instellen. Experimenteer er even mee.)
► Hoe had je zelf die vergelijking algebraïsch kunnen vinden?
► Maak de lijn AB onzichtbaar. (Dat doe je door met de rechter muisknop op de lijn te klikken en Object tonen uit te zetten.)
► Maak driehoek ABC met C(7,5). (Dat kan op verschillende manieren: bijvoorbeeld door via de knop [Veelhoek] te kiezen voor Veelhoek en dan vervolgens A, B aan te klikken en op de juiste plek te klikken voor C en vervolgens de driehoek af te maken door weer op C te klikken. Maar je kunt ook gewoon eerst punt C maken en dan na de keuze Veelhoek achtereenvolgens op A, B, C en weer op A te klikken. En tenslotte kun je ook gewoon de drie punten A, B en C verbinden met lijnstukken, maar daarvan is het nadeel dat er dan geen object “driehoek” is.)
► Bepaal de omtrek en de oppervlakte van de driehoek. Breng die getallen in beeld. (Werk met de rechter muisknop en Eigenschappen op elk object, kies Label tonen, Naam en waarde. Om de omtrek in beeld te krijgen moet je de lengtes van de drie zijden optellen – voer in p=a+b+c – en dan via [Schuifknop] en kiezen Tekst invoegen de tekst gaan typen: omtrek(ABC) = waarna je bij geavanceerd de p kunt toevoegen. Na [Enter] zie je dan de tekst.)
► Je kunt de drie hoekpunten verplaatsen met de knop [Verplaatsen]. Ga na, dan omtrek en oppervlakte mee veranderen.
► Sla je werk op als 2-1-voornaam-achternaam.ggb
Loodlijn, deellijn, middelloodlijn, zwaartelijn
► Teken een loodlijn door B op AC.
(Kies Loodlijn, klik op B en op b en daar staat ie.)
► Teken de hoogtelijn BD met punt D op AC.
(Je hebt al een loodlijn getekend. Benoem het snijpunt van die loodlijn met AC via [Nieuw punt] en Snijpunt van twee objecten. Klik zowel b als de loodlijn g aan. Je hebt nu punt D. Maak vervolgens de loodlijn onzichtbaar en teken lijnstuk BD.)
► Teken de rechte hoek teken bij D.
(Kies voor [Hoek] Hoek en klik op B, D en C in die volgorde. Kijk ook wat er gebeurt als je een andere volgorde kiest.)
► Teken de deellijn van hoek A.
(Kies voor [Loodlijn] Bissectrice en klik vervolgens op B, A en C in die volgorde. Kijk ook wat er gebeurt als je een andere volgorde kiest.)
► Teken de middelloodlijn van AC.
(Kies voor [Loodlijn] Middelloodlijn en klik vervolgens op A en C. En alweer klaar, of wil je er nog een rechte hoek teken inzetten? Bedenk zelf hoe je dit doet.)
► Teken de zwaartelijn door A.
(Kies voor [Nieuw punt] Midden of middelpunt en klik vervolgens op B en C. Je hebt nu het midden van BC. Teken vervolgens een lijn door dit midden en door punt A.)
► Sla je werk op als 2-2-voornaam-achternaam.ggb
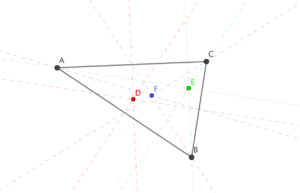
De rechte van Euler
Probleemstelling:
Welke eigenschap hebben het snijpunt van de drie hoogtelijnen, het snijpunt van de drie zwaartelijnen en het snijpunt van de drie middelloodlijnen van een driehoek?
► Open een nieuw GG werkblad. Maak een driehoek ABC.
► Maak de drie genoemde punten en formuleer een vermoeden. Verklaar de titel van 2.3.
► Voldoet het snijpunt van de drie bissectrices ook aan deze eigenschap?
► De verklaring, het bewijs, is voor een meetkundemodule.
► Sla je werk op als 2-3-voornaam-achternaam.ggb
Constructie parabool
Probleem:
Construeer de verzameling van alle punten die even ver af liggen van een horizontale lijn en een punt F dat boven die lijn ligt. Zo’n verzameling heet een meetkundige plaats. De meetkundige plaats van deze punten heet parabool: probeer de formule ervan te verklaren.
► Open een nieuw GG werkblad. Teken een horizontale lijn r. Teken er een punt F boven. (Rechter muisknop op een object, kies Naam wijzigen en geef het de naam die je wilt.)
► Maak een punt R op de lijn.
(Kies voor [Nieuw punt] Punt op object en klik op de horizontale lijn die je hebt gemaakt.)
► Teken een loodlijn door R op r.
► Teken de middelloodlijn van FR.
► Benoem het snijpunt van de middelloodlijn van FR en de loodlijn op r. Noem dit punt P.
► Laat zien dat voor dit punt geldt FP = PR.
► Zet van punt P het “spoor” aan. (Rechter muisknop op P en Spoor aan.)
► Beweeg punt R over lijn r en zie de parabool ontstaan.
► Maak met GG een parabool bij lijn r en punt F.
(Kies [Ellips] Parabool en klik op r en F. Je zult zien dat deze parabool samenvalt met het puntenspoor dat je hebt gemaakt.)
► Als je dit doet met de lijn y = -1 en punt F(0,1) krijg je de parabool y =0,25 x2. Ga maar na.
► Sla je werk op als 2-4-voornaam-achternaam.ggb