Leerdoelen

De leerling is in staat om de verworven kennis van de functionaliteit van Geogebra toe te passen in de open onderzoeksopdracht.
De leerling is in staat om keuzes te maken in de mate van begeleiding.
De leerling kan algebraïsch een kwadratisch verband aantonen.
De leerling is in staat aan de hand van gegeven formules wiskundig te redeneren.

AFSPRAAK OVER NAAMGEVING BESTANDEN

Aan het eind van deze pagina kun je je antwoorden uploaden. Je zult altijd één, of meer GeoGebra bestanden en één Word, of PDf bestand met antwoorden op vragen hebben. Alle vragen/acties gemarkeerd met een ► dienen uitgevoerd te worden en vastgelegd in een WORD of PDF bestand

Bewaar je GeoGebra bestanden als 17-baansnelheid–1.ggb en 17-baansnelheid–2.ggb etc.
Bewaar je Word/Pdf bestand met antwoorden als 17-baansnelheid.doc(x) en/of 17-baansnelheid.pdf .

Veel succes!

De opdracht begint hier:

► Bekijk: https://nl.wikipedia.org/wiki/Kogelbaan
► Open Kogelbaan.ggb

In dit bestand is uitgegaan van de formules:

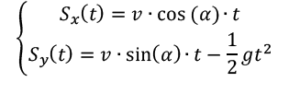
(waarin g≈9,81 m/s^2 de valversnelling is) Verder wordt het traject dat een kogel aflegt nagebootst (na t seconden, afgeschoten vanaf een vlakke ondergrond op een hoogte h, onder een hoek α met een mondingssnelheid v van het vuurwapen). Hierbij is de luchtweerstand verwaarloosd.

► Onderzoek welke hoek het optimale bereik van het vuurwapen geeft en probeer dit wiskundig te verklaren door een vergelijking op te lossen (te simuleren door de schuifknop t te variëren).
Het lijkt erop dat de baan altijd een parabolisch traject volgt.

► Laat dit zien door uit bovenstaande parametervergelijking de variabele t te elimineren.
► Probeer het bestand zodanig aan te passen dat er geschoten wordt vanaf een hellende ondergrond.
► Probeer dit ook in Geogebra vorm te geven. Maak hierbij gebruik van de gegeven site en je kunt voor hints terecht op deze website.
► Onderzoek en beschrijf wat er met de baan van de kogel gebeurt indien er wel rekening wordt gehouden met de luchtweerstand. Koppel dit aan wat je hebt geleerd bij het onderdeel kegelsneden.
► Kun je binnen Geogebra ook een kogelbaan simuleren door rekening te houden met de luchtweerstand? (Hint: Die is recht evenredig met de snelheid van het voorwerp!)

Upload je bestanden hier

[wordpress_file_upload singlebutton=”true” dragdrop=”false” uploadrole=”all” uploaduser=”all” uploadpatterns=”*.pdf, *.doc, *.docx, *.ggb” forcefilename=”true” duplicatespolicy=”maintain both” placements=”filename+selectbutton/progressbar/subfolders/filelist” uploadtitle=”Upload bestanden” selectbutton=”Selecteer bestanden/Selecteer bestanden” uploadbutton=”Selecteer bestanden/Selecteer bestanden”] [wordpress_file_upload_browser pagination=”false” bulkactions=”false” candownload=”true” candelete=”true” deletestrictmode=”true” columns=”file:s/File,date:n/Upload Date,user:s/User,link:/Link” postfilter=”current”]